컴퓨터에서 사용하는 수는 크게 정수와 실수로 나뉘며, 이에 따라 컴퓨터에서의 표현 방식도 완전히 달라진다.
정수 : 소수점 이하의 값을 갖지 않는 수 ex ) 126 또는 -126은 정수 , 126.00 또는 -126.00은 정수가 아니다.
또한 컴퓨터에서는 무한한 범위의 수를 표현하기 위해서는 무한한 양의 메모리가 필요하므로 실제로는 제한된 범위, 즉 정수표현을 위해서 할당된 메모리가 허용하는 범위만큼의 정수만을 표현할 수 있다.
이런 정수를 표현하는 방식은 크게 , 부호 없는 정수 (unsigned integer)와 부호 있는 정수 (signed integer)로 나뉜다.
1). 부호 없는 정수
부호 없는 정수에는 부호 ( +, - )를 표시하는 비트가 존재하지 않는다. 따라서 음의 정수는 표현할 수 없다.
n비트가 할당된 부호 없는 정수의 범위는 0부터 2^n-1( 2의 n제곱 -1 )까지이다.
ex) 8비트 정수 : 0부터 255까지
부호 없는 정수로 표현하는 과정
- 주어진 수를 2진수로 변환하고 변환된 2진수를 할당된 n비트에 채우면 된다.
- 변환된 2진수의 비트의 개수가 할당된 비트의 개수 n보다 큰 경우에는 주어진 값을 할당된 n비트로 표현할 수 없게 된다.
- 이런 경우를 오버플로 ( overflow )라고 한다.
ex ) 10진수 275를 8비트 부호 없는 정수로 표현
1. 275를 2진수로 변환 -> 100010011 ( 9자리 )
해당 데이터를 표현하기 위해서는 결국 9비트가 필요하게 되는데, 할당된 8비트로는 모두 담아낼 수 없다.
따라서 오버플로가 발생한다. ( 8비트가 표현할 수 있는 최대의 수는 255 )
초과하는 정수를 나타내기 위해서는 8비트 보다 더 많은 비트가 필요하다.
2). 부호 있는 정수
n비트를 사용하는 부호 있는 정수 표현 방법에서는 할당된 n비트 중에서 최상위 1비트 ( MSB : Most Significant bit )는
부호비트로 사용하고 나머지 ( n-1 ) 비트는 주어진 정수의 크기를 나타내는 데 사용한다.
부호비트가 0 이면 양의 정수
부호비트가 1 이면 음의 정수
부호 있는 정수를 표현하는 방법에는 부호화 - 크기 ( signed magnitude ) 방식, 1의 보수 방식, 2의 보수 방식이 있다.
1. 부호화-크기 방식
n비트로 표현되는 부호화-크기 방식에서는 주어진 음의 정수에 대해 절댓값을 취해서 표현하기 때문에 부호 비트를 제외하면 나머지 비트는 양의 정수 이든 음의 정수이든 상관없이 동일한 형태로 표현된다.
ex )
8비트로 124를 표현하는 경우
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
< 부호 비트 >
8비트로 -124를 표현하는 경우
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
< 부호 비트 >
이 방식에서 n비트로 표현할 수 있는 수의 범위는, 부호 비트로 1비트가 제외되고 (n-1) 비트로만 수를 나타내기 때문에
-(2^n-1 - 1)~ + ( 2^n-1 -1)이 된다.
또한 8비트 부호화-크기 방식에서 0은 00000000이 되고, 10000000로도 표현할 수 있다.
이는 +0과 -0을 표현하는 것이다.
결과적으로 양수와 음수의 범위는 정확히 대칭을 이루며, 데이터가 ±n 인지를 검사해야 하는 문제점을 갖다.
2. 1의 보수 방식
1의 보수 방식은 기본 아이디어는 양의 정수에 대한 보수로서 음의 정수를 표현하는 것이다. 음의 정수의 표현은 양의 정수에 대한 표현에서 0은 1로 1은 0으로 바꾸면 된다.
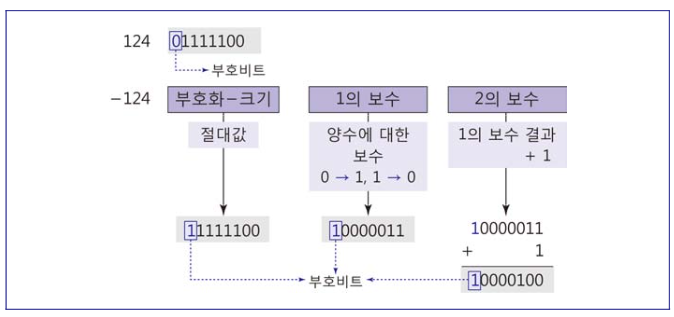
ex) -124를 8비트의 1의 보수 방식으로 표현
1). 124에 대한 이진 표현 -> 01111100
2). 01111100에서 1의 보수 방식 적용 -> 10000011
3). 결과적으로 -124에 대한 1의 보수 방시의 최종표현은 10000011이 된다.
1의 보수 방식에서 표현할 수 있는 수의 범위는 부호화-크기 방식에서와 동일하며, 마찬가지로 +0과 -0의 두 가지 표현을 갖는다는 문제점이 있다.
3. 2의 보수 방식
2의 보수 방식에서 음의 정수는 1의 보수 방식으로 계산한 결과에 1을 더해서 표현한다.
ex) -124를 8비트의 2의 보수 방식으로 표현
1). -124에 대한 1의 보수를 계산 -> 10000011
2). 1)에 대한 결과 값에 +1 ->
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| + | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
3). 최종적으로 -124에 대한 2의 보수 방식에 대한 표현 결과는 10000100
1,2와 달리 2의 보수 방식에서는 하나의 0만 존재한다.